Движение гарпуна в водной среде
«Давайте не будем философствовать, а просто посчитаем…»
Рене Декарт
1. Вступление.
Целью данной работы является получение и анализ зависимостей скоростей, координат и кинетической энергии движения гарпуна выпущенного горизонтально в водной среде, а также изучение влияния изменения параметров гарпуна и линя на движение гарпуна. Сделанные выкладки предполагают быть доступными для большинства подводных охотников, которые смогут также воспользоваться и приложенным файлом (Exel) для проведения собственных расчетов.
Без учета сопротивления среды задача о теле, брошенном горизонтально или под углом к горизонту, проиллюстрирована во многих, даже школьных учебниках. Учет сопротивления воздуха при расчетах траектории полета снарядов хорошо исследован в баллистике [1]. Формулы, выражающие сопротивление воздушной и водной сред, хотя и похожи, но подходы воздушной баллистики для водной среды не приемлемы.
Гидродинамика – сложная и самодостаточная наука, которая дает возможность построить искомую модель. В литературе [2-4] приведены методы расчета сил, которые возникают при движении в жидкой среде, но исследование кинематических величин и построение траектории движения тел не проведено. Разумеется, что при создании огнестрельного оружия для подводных пловцов подобные расчеты проводились, но они не опубликованы в открытой печати. В [3] приведены методы расчета параметров подводного движения баллистических ракет, но из-за сложности и громоздкости их применение для нашей задачи затруднительно. Несколько упрошенное рассмотрение зависимостей скорости и координаты от времени движения приведено в [5], но полученные там зависимости не учитывают форму тела. Учитывая изложенное, перед работой не ставится задача выяснения абсолютной истины в особенностях подводного движения тел – мы попытаемся как можно полнее проанализировать движение гарпуна подводного ружья, пользуясь при этом математическим аппаратом, который будет понятен широкому кругу читателей.
2. Объект исследования и его взаимодействие со средой.
В качестве базового объекта исследования выберем гарпун длиною l= 76 см, диаметром d= 8 мм, передняя его часть имеет форму конуса. Также нам понадобятся плотность материала, из которого он изготовлен – pм= 7800 кг/м3 (сталь) и 4540 кг/м3 (титан); плотность воды – p =1000 кг/м3;
вязкость воды n = 10-3 Па·с уже будет учена в формуле силы сопротивления. К гарпуну привязан линь диаметром 2 мм.
Заметим, что внутренняя баллистика выстрела, то есть особенности разгона и движение гарпуна до его выхода из ружья (отделения от ружья) в работе будут исследованы лишь частично.
Движение гарпуна можно рассматривать как два независимых: горизонтальное и вертикальное. Реальное движение будет суперпозицией двух указанных.
В горизонтальном направлении на гарпун действует сила гидродинамического сопротивления, которая состоит из трех составляющих: силы лобового Fл и донного Fд сопротивлений, силы трения боковой поверхности Fпов (см. рис. 1). Первые две принято объединять в одну:
где S* – площадь наибольшего поперечного сечения гарпуна, перпендикулярного к направлению движения; p – плотность води; v –скорость движения; Сх – коэффициент формы. С использованием формулы (1) можно с успехом рассчитывать силу сопротивления для объектов элементарной формы: шара, конуса, цилиндра. При этом коэффициент формы Сх равен: для шара – 0,47; для конуса 0,50; длинного цилиндра при продольном обтекании – 0,82, а при поперечном – 1,2.
Сила трения боковой поверхности так же, как и первая, пропорциональна квадрату скорости:
где S – площадь боковой поверхности, k – коэффициент пропорциональности. Эта составляющая силы, согласно критерию Рейнольдса станет пропорциональна первой степени скорости лишь при
движении со скоростью меньшей 1 см/с, обеспечив при этом почти мгновенную остановку.
Не скроем, мы проводили расчеты и в предположении, что сила поверхностного трения пропорциональна первой степени скорости на всем пути движения гарпуна, но полученные результаты не подтверждаются экспериментально. Кроме того, это противоречит критерию Рейнольдса для объектов таких размеров и используемых скоростей.
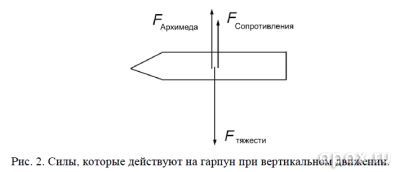
При вертикальном движении тела на него действует система сил (см. рис. 2).
Поскольку плотность гарпуна больше плотности воды, то сила тяжести превышает силу Архимеда – начинается движение из состояния покоя ускорено вниз. При увеличении скорости увеличивается и сила сопротивления среды. Но наступает тот момент, когда сила тяжести уравновешивается суммой сил Архимеда и сопротивления среды, тогда гарпун начинает двигаться с постоянной скоростью.
3. Математические модели.
3.1. Горизонтальное движение гарпуна.
В работе [4], сила гидродинамического сопротивления представлена как сумма зависимостей (1) и (2) в удобном для расчетов виде:
где Сх= 0,5 – коэффициент формы для конуса, l – длина гарпуна, d – диаметр, S* – площадь поперечного сечения, P – плотность воды, v – скорость движения объекта.
Его решение и последующая математическая обработка дает нам зависимость горизонтальной скорости от времени:
Vo – начальная скорость, m – масса гарпуна, Сх= 0,5 – коэффициент формы для конуса, l – длина
гарпуна, d – диаметр, S* – площадь поперечного сечения, p – плотность воды.
Уравнение (4) можно решить и относительно координаты, при этом получим зависимость скорости от координаты. Проинтегрировав выражение (5) получим зависимость координаты от времени. Как хорошо ни решаются эти уравнения, и какие красивые зависимости ни получаются, влияние линя в
них не учтено.
Учет влияния линя на полет гарпуна требует более серьезного подхода, так как к силе сопротивления гарпуна добавится сопротивление линя. Если dЛ – диаметр линя, х – длина размотанной части линя, S’ – площадь поперечного сечения линя, то уравнение (4) примет вид:
Решение этого уравнения дает нам зависимость горизонтальной скорости от координаты:
vo – начальная скорость гарпуна, m – масса гарпуна, Сх= 0,5 – коэффициент формы для конуса, l – длина гарпуна, dГ – диаметр гарпуна, S* – площадь поперечного сечения гарпуна, dЛ – диаметр линя, х – длина размотанной части линя, S’ – площадь поперечного сечения линя, P – плотность воды.
Координату от времени выразить в элементарных функциях не удается, но приведенный ниже интеграл вполне можно подсчитать и числовым методом, даже с помощью таблиц Exel (файл прилагается).
где xn – граница интегрирования, которая изменяется от нуля до максимальной исследуемой дистанции
Формулу (8) можно использовать для расчета времени подлета гарпуна к мишени, добавив время движения гарпуна в стволе, которое рассчитывается в следующих приближениях.
Пускай со стороны поршня (резиновых тяг) действует постоянная сила, то есть нужно найти среднее арифметическое между начальной и конечной силами. Для пневматического ружья изменение силы находится в пределах 5%, что вполне приемлемо для наших расчетов. Для арбалета такой подход менее приемлем, поскольку сила упругости тяг изменяется не по линейному
закону. Не будем учитывать силу сопротивления выгоняемой из канала ствола воды и трение поршня, поскольку это приведет к необходимости учета конструктивных особенностей ружья и сильно затруднит расчеты.
Указанные допущения позволяют с точностью до 15% определить время движения гарпуна в стволе, решая следующее уравнение:
Его решение дает формулу:
где
F – средняя сила, приложенная к гарпуну со стороны поршня, vo - скорость гарпуна при вылете из ствола (начальная скорость), m – масса гарпуна, Сх= 0,5 – коэффициент формы для конуса, l - длина гарпуна, dГ – диаметр гарпуна, S* – площадь поперечного сечения гарпуна, P – плотность воды.
Кинетическая энергия рассчитывается по формуле
Учитывая то, что скорость горизонтального движения гарпуна на дистанции уверенного поражения намного превышает вертикальную, в формулу расчета кинетической энергии подставляем значение горизонтальной скорости.
3.2. Вертикальное движение гарпуна.
В вертикальном направлении на гарпун действует сила тяжести и противоположные к ней: сила Архимеда
(P – плотность воды, g= 9,8м/с2 – ускорение свободного падения, V – объѐм тела) и сила сопротивления водной среды
(см. рис. 2). Коэффициент формы Сх= 1,2, так как в этом случае обтекание происходит в перпендикулярном к оси цилиндра направлении и S, соответственно, – площадь осевого (продольного) сечения цилиндра, v – скорость движения гарпуна.
Равнодействующая этих сил
определяет положительное ускорение движения тела. Воспользовавшись вторам законом Ньютона, запишем дифференциальное уравнение:
Его решение и последующая математическая обработка дают нам искомые зависимости вертикальной скорости и координаты от времени.
m – масса гарпуна, Сy= 1,2 – коэффициент формы для цилиндра при поперечном
обтекании, l – длина гарпуна, d – диаметр, S – площадь осевого (продольного) сечения, P – плотность воды, g= 9,8м/с2 – ускорение свободного падения.
3.3. Траектория движения гарпуна.
Учитывая сложность выражения горизонтальной координаты от времени, следует провести расчет интеграла (8), получив при этом зависимость t(x). Подсчет y(t) провести от полученного времени t(x), а для построения взять колонки x и y(t).
Как мы видим все расчеты можно произвести не прибегая к помощи языков программирования.
4. Анализ полученных результатов.
4.1. Общие замечания.
И все-таки, какие физические величины следует поставить во главу угла при сравнении различных конструкций гарпунов? Прежде всего, следует постулировать, что все исследуемые гарпуны получают от ружья одинаковую энергию, то есть имеют одинаковую начальную кинетическую энергию.
Примем ее равной 108 Дж, что будет соответствовать начальной скорости 27 м/с стального гарпуна массой 300 г, длиной 76 см и диаметром 8 мм (базового объекта). Физической величиной, отвечающей за проникновение объекта в вязкую среду (рыбу), является кинетическая энергия. Но энергией в 108 Дж может обладать и лом, движущийся со скоростью десяток сантиметров в секунду. Результат его попадания в рыбу предсказуем – мы даже подранка не сделаем. Поэтому кроме энергии гарпуна следует учесть и скорость, с которой он будет подходить к объекту охоты. При выборе минимальной скорости мы опирались на наши экспериментальные данные полученные при охоте на кефаль. Практика показывает, что наш базовый объект при скорости менее 7 м/с, уже не способен нанести поражающего действия. Примем эту скорость и соответствующую ей кинетическую энергию 7,35 Дж за граничные значения, ниже которых, гарпун уже не способен поразить рыбу. Естественно, для других объектов охоты указанные величины будут другими, но желающие провести соответствующую коррекцию смогут сделать это и сами.
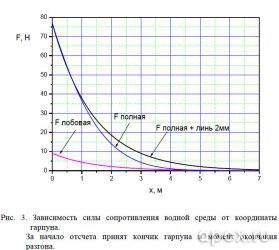
Так на сколько же велика сила сопротивления водной среды? Из рисунка 3 следует, что максимальная сила составляет 77 Н, или 7,86 кгс. Сила лобового сопротивления гарпуна невелика, и составляет 12% от полной силы сопротивления, действующей на гарпун. Также можем видеть, что линь вносит существенный вклад в силу сопротивления всей системы гарпун-линь. На расстоянии 2 м его доля – 25%. На этом графике и на многих последующих за начало отсчета принято острие гарпуна в момент окончания разгона. Поэтому тем, кто хочет знать полную дистанцию стрельбы, следует добавить к координате расстояние от ручки ружья до кончика гарпуна, вставленного в ружье без проведения зарядки.
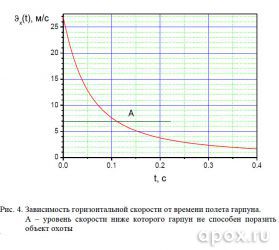
Следующий график (см. рис. 4) говорит нам о том, что процесс полета гарпуна до падения скорости ниже критической величины занимает 110 миллисекунд. Добавив время движения гарпуна в стволе – 36 мс, получим 146 мс – общее время выстрела и полета, или 0,146 с. Недолго длится выстрел из идеального ружья! Почему идеального? Да потому, что мы не учитываем время срабатывания спускового механизма и достижения силой стандартного значения, а также трение поршня о ствол и сопротивление воды при выходе из канала ствола. Но как показывает практика, правильно сконструированное ружье нивелирует эти влияния.
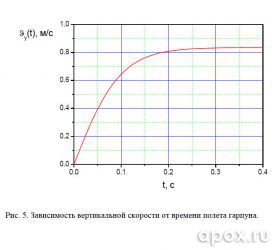
Интересна и зависимость вертикальной скорости, представленная на рисунке 5. Сопоставив графики 4 и 5, видим, что до времени 0,11 с – момента падения скорости ниже критической, График траектории полета гарпуна (см. рис. 6) можно использовать при расчете возвышения прицельной планки рожкового прицела и предварительной юстировки коллиматорного или лазерного прицелов.
Указанное стрелкой направление обеспечивает отклонение гарпуна от заданного менее чем 1,5 см на дистанции до 4-х метров, что говорит, о принципиальной возможности (а не целесообразности) применения любого рода подводных прицелов. вертикальная скорость так и не успевает набрать своего максимального значения 83,5 см/с.
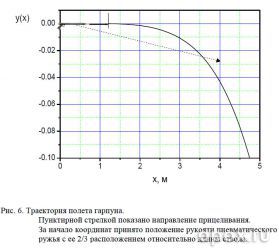
График траектории полета гарпуна (см. рис. 6) можно использовать при расчете возвышения прицельной планки рожкового прицела и предварительной юстировки коллиматорного или лазерного прицелов. Указанное стрелкой направление обеспечивает отклонение гарпуна от заданного менее чем 1,5 см на дистанции до 4-х метров, что говорит, о принципиальной возможности (а не целесообразности) применения любого рода подводных прицелов.
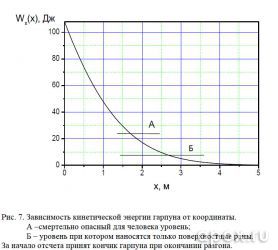
Раз уж мы имеем дело с оружием то нелишним будет знать, на каком расстоянии оно опасно для человека, плывущего в воде. В литературе [6, 7] указано, что объект выстрела с удельной энергией 50 Дж/см2 выводит из строя человека, даже при попадании в грудную клетку, а при 15 Дж/см2 наносит лишь поверхностные раны. Выбранный нами в качестве стандартного гарпун должен иметь кинетическую энергию в 25,13 и 7,54 Дж соответственно (см. рис. 7).
Таким образом, на расстоянии менее 1,7 м (не забываем добавить расстояние от рукояти до кончика гарпуна в момент окончания его разгона) гарпун с начальной кинетической энергией 108 Дж представляет смертельную опасность для человека, а после 2,67 м все еще может нанести
поверхностные раны.
Приятной неожиданностью для нас стало то, что расчетная граничная энергия гарпуна, ниже которой наносятся только поверхностные раны, оказалась приблизительно равной уровню, который получен нами экспериментальным путем – 7,54 Дж и 7,33 Дж, соответственно.
4.2. Варьирование параметрами гарпуна.
4.2.1 Изменение плотности материала гарпуна.
Давайте сравним наш стандартный стальной гарпун с возможными альтернативными, тех же размеров и геометрической формы. Первым претендентом на альтернативу является титан. Благодаря невысокой плотности (4540 кг/м3) этот объект будет иметь массу 173 г и, согласно
закону сохранения энергии, начальную скорость 35,3 м/с. Близкие к нему параметры имеет чудо-продукт «нанотехнологий» – углепластиковый гарпун, которым ведущие фирмы-производители подводного оружия пытались заменить «морально устаревшие» стальные. Для увеличения средней плотности мы предлагаем рассмотреть, как вариант, стальной гарпун со свинцовым сердечником. Если в стандартном гарпуне диаметром 8 мм высверлить отверстие диаметром 6 мм, и залить его свинцом, то плотность такого объекта окажется равной 9750 кг/м3. Его масса вырастет до 372 г, а скорость уменьшится до 24,1 м/с. О механических свойствах такой
«инновации», а также о возможности замены свинца на слабо обогащенный уран, мы скромно умолчим.
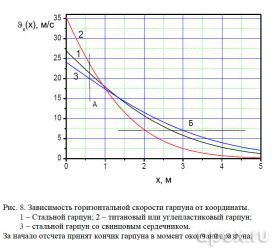
На рисунке 8 показаны зависимости горизонтальной скорости этих образцов от координаты.
Рассмотрим дистанцию до 1 м, понимая при этом, что расстояние до рукоятки ружья составит порядка 2,2 м. На срезе А скорость легкого гарпуна превысит принятую нами за стандарт на 11%, а утяжеленного – на 6% ниже стандартной. Если оценить дистанцию, на которой скорость станет ниже критической (показана уровнем Б), то увидим, что титановый гарпун проигрывает в убойной дистанции на целых 70 см, а со свинцовым сердечником выиграет у стального на 30 см.
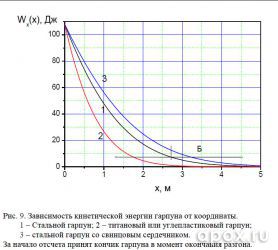
Ситуация с кинетической энергией, показанная на рисунке 9, также говорит не в пользу легких гарпунов – убойная дистанция сокращается на метр и на всем протяжении полета титановый проигрывает стальному.
А вот утяжеленный гарпун увеличивает убойную дистанцию на 50 см и показывает лучшие результаты по энергии на всем пути. Это «лучшие» составляет то 0 до 28%.
Если взять критическую дистанцию стрельбы для стандартного гарпуна (2,7 м), то гарпун со свинцовым сердечником в этой точке будет иметь на 70% большую кинетическую энергию, что является существенной прибавкой, которая позволит пробить более плотную, чем взятую нами за
основу кефаль, рыбу.
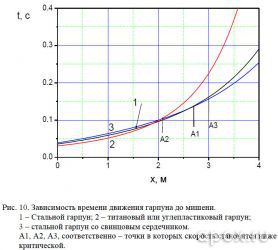
Логичным будет предположить то, что гарпуны, имея различные массы, будут различаться по времени движения гарпуна в стволе и в полете. Суммарное время выстрела и полѐта представлено на рисунке 10.
Да, действительно, легкий гарпун быстрее достигает цели. В процентном отношении это выглядит впечатляюще – 15% при координате 1 м (для определения истинной дистанции стрельбы, не забываем добавить расстояние от кончика выходящего из ствола гарпуна до рукоятки ружья). Но
абсолютная величина этого преимущества составляет всего 0,008 с . Если испуганная рыба начинает убегать перпендикулярно направлению выстрела со скоростью 5 м/с, то точка попадание гарпуна будет смещена на 4 см меньше чем у стального гарпуна. Каждому охотнику решать самому – существенно ли это для его условий охоты.
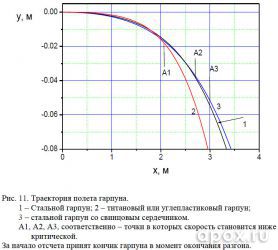
Графики траектории движения гарпунов, показанные ни рисунке 11, говорят о том, что на расстоянии уверенного поражения самого легкого гарпуна (А2), определяемого уровнем критической скорости, ни один гарпун не имеет преимущества.
Да и в дельнейшем движении стального и начиненного свинцом гарпунов прослеживается та же тенденция.
Подводя итоги исследований связанных с изменением плотности материала гарпунов, можно констатировать, что ни во времени движения, ни в его траектории нет чемпионов. Титановый или углепластиковый гарпуны проигрывают в кинетической энергии, сокращая свою убойную дистанцию на 1 м, а гарпун со свинцовым сердечником увеличивает ее на 30-50 см, показываю лучшие результаты по энергии на всем протяжении полета.
Таким образом, применение легких материалов при изготовлении гарпуном нецелесообразно, ведь преимущество при этом достигается незначительное, использование возможно только на коротких дистанциях, а себестоимость таких гарпунов – высокая. Мы не открыли Америку установив, что начинив гарпун свинцовым сердечником будут получены лучшие результаты, но прежде чем преступать к изготовления такого снаряда, следует хорошо взвесить соотношение затрат и улучшения боевых качеств полученных гарпунов.
Изменение силы отдачи, при использовании различных по массе гарпунов, не должно происходить, поскольку согласно третьему закону Ньютона она зависит лишь от величины давления в ресивере или силы натяжения резиновых тяг.
4.2.2. Изменение диаметра гарпуна.
Наиболее часто используемый в пневматических ружьях диаметр гарпуна – 8 мм. Но наряду с этим применяются гарпуны диаметром 7 и 9 мм. В арбалетах стараются применять гарпуны как можно меньшего диаметра, а его увеличение производят только из механических соображений – мощные тяги заставляют длинные гарпуны совершать немалые колебания. И все же мы рассмотрим влияние изменения диаметра гарпуна на его боевые характеристики, особо не вдаваясь в особенности конструкций ружей.
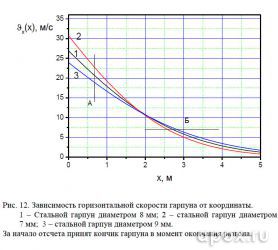
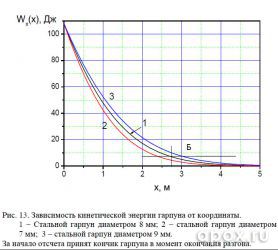
Анализ скорости движения (см. рис. 12), показывает преимущество тонкого гарпуна на дистанции до 1,9 м (срез А), но, вместе с тем, он проигрывает в кинетической энергии на всем протяжении полета (см. рис. 13), уменьшая при этом убойную дистанцию на 20 см . Незначительное уменьшение
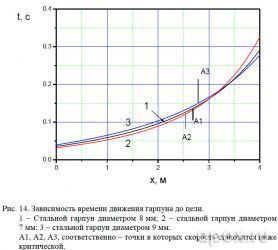
времени полета есть (см. рис. 14), но как показано в пункте 4.2.1 большего эффекта это не принесет. А вот толстый гарпун, показывая лучшие результаты по кинетической энергии, увеличивает дистанцию уверенного поражения на 20 см. Если взять критическую дистанцию стрельбы для стандартного гарпуна (2,7 м), то гарпун диаметром 9 мм в этой точке будет
иметь на 36% большую кинетическую энергию.
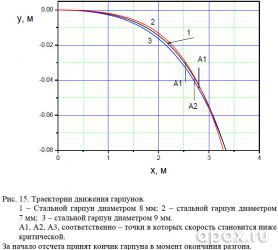
Исследуя траектории движения, показанные на рисунке 15,констатируем их абсолютную идентичность, ведь отличие составляет считанные миллиметры.
Таким образом, применение более толстого гарпуна можно с уверенностью рекомендовать для охоты на рыбу, пробивание которой требует больших затрат энергии, например на сазана. В то же время бесцельно уменьшать диаметр, на наш взгляд не целесообразно. В его уменьшении есть смысл лишь при охоте на мелкую рыбешку на небольшой дистанции, так как тонкий гарпун имеет меньшее сопротивление проникновения в ткани рыбы и, оставляя меньшую рану, снижает
вероятность разрыва добычи.
4.2.3. Изменение длины гарпуна.
Наш стандартный гарпун имеет длину 76 см. Проведем сравнение его характеристиками гарпунов длиною 60 см и 95 см. Мы выбрали именно такие изменения длины, поскольку полученные изменения массы при этом будут соизмеримы с изменениями массы, рассмотренными в пункте 4.2.2 при варьировании диаметром гарпунов.
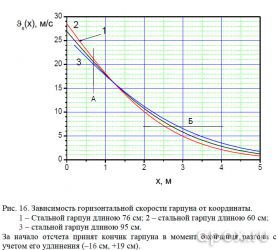
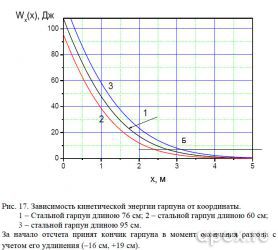
Проводя анализ графиков, представленных на рисунках 16 и 17, можно констатировать нецелесообразность уменьшения длины гарпуна. Это приводит к значительному уменьшению кинетической энергии, хотя потери в скорости на дальних дистанциях выглядят не так угрожающе. Увеличение длины на 19 см приводит к ощутимой прибавке в кинетической энергии, но здесь следует понимать и причину такого увеличения. В значительной мере эта прибавка связана с перенесением начала отсчета на 19 см вперед, хотя увеличение наблюдается и относительно несмещенного начала отсчета.
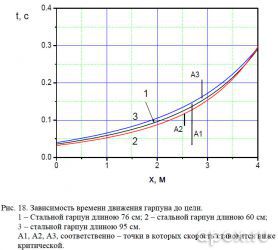
Анализируя подлетное время видоизмененных по длине гарпунов, как и ранее, приходим к выводу, что его изменение не приведет к существенным различиям в результатах стрельбы (см. рис. 18).
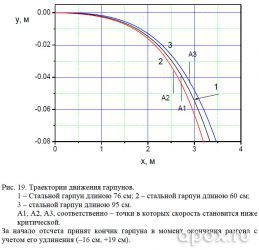
Траектория движения самого массивного гарпуна, представленная на рисунке 19, несколько ярче отличается от траекторий, полученных варьирований плотностью и диаметром, хотя проседание его на дистанции 2,7 м всего на 5 мм меньше чем стандартного.
Таким образом, удлинение гарпуна можно проводить с целью увеличения дистанции уверенного поражения. Эта необходимость может возникнуть при изменении условий охоты – выход из зарослей и коряг на открытую воду, или улучшение видимости.
4.3. Анализ результатов, полученных при варьировании параметрами гарпунов и выбор наилучшего изменения.
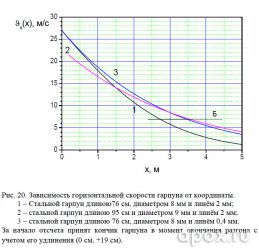
Как показывают исследования, проведенные в разделе 4.2, лучшие результаты дают гарпуны увеличенной массы. Поскольку заметных изменений во времени подлета не наблюдается, то этот график не будем показывать при обобщении результатов. Разумеется, что наилучшие результаты покажет гарпун, у которого увеличение массы будет проведено по трем параметрам: толщине, длине и плотности. При сохранении толщины стенок 1 мм, получаем диаметр свинцового сердечника – 7 мм, массу гарпуна – 595 г и среднюю плотность – 9852 кг/м3. Такой гарпун увеличивает убойную дистанцию до 4 м, считая от его кончика в момент окончания разгона. Но, как уже упоминалось, изготовление его требует достаточно серьѐзных затрат. Следующий за ним результат показывает утолщенный и удлинѐнный гарпун, увеличивая дистанцию уверенного поражения до 3,52 м, что на 82 см больше чем у стандартного (см. рис. 20).
Но как показывают расчеты, почти такого же результата можно добиться, уменьшив диаметр линя с 2 мм до 0,4 мм. Если мы охотимся на сома, то такая замена не оправдана – никто не стреляет его с 4-5 метров, да и такой толщины линь будет обязательно порван. А вот в морской охоте на максимальной дистанции такой подход может быть очень полезен. Лобан или горбыль массой 1-2 кг не способны порвать современную леску диаметром 0,4 мм. Недостаток тонкой лески в том, что она легко режет мясо рыбы, оставляя подранка. Но этого можно избежать, пойдя на компромисс –
поставив после гарпуна участок 2-х миллиметрового линя длиною 30-50 см.
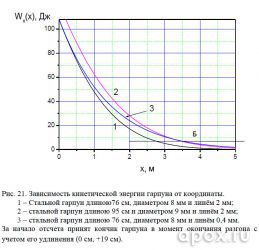
Практически та же ситуация прослеживается и в кинетической энергии (см. рис. 21). Пускай энергия стандартного гарпуна, но с тонким линем и меньше, чем у тяжелого на всем протяжении убойной дистанции, но ее уровень все равно выше критического, а значит охота на кефаль – открыта!
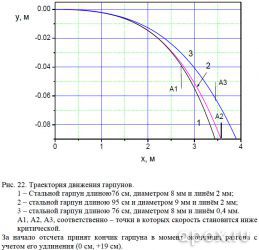
Еще неожиданнее выглядят траектории гарпунов-победителей (см. рис. 22). Незначительно проигрывая в убойной дальности, стандартный гарпун с тонким линем почти на 3 см меньше отклоняется от прямолинейной траектории, чем утяжеленный. Этот факт так же следует занести в счет побед тонкого линя.
Подводя итоги анализа результатов варьирования параметрамигарпуна, можно с уверенностью сказать следующее.
- Уменьшать массу гарпуна нецелесообразно ни за счет длины или диаметра гарпуна, ни за счет применения титана или улепластика.
- К наилучшим результатам по увеличению дальности поражения и кинетической энергии гарпуна приводит применение гарпуна со свинцовым сердечником; следом за этим идут результаты полученные при увеличении диаметра и длины цельностального гарпуна.
- Одновременное утолщение и удлинение гарпуна дают наилучшие результаты по увеличению убойной дистанции, с учетом себестоимости изготовления гарпуна.
- Уменьшением толщины линя можно достичь таких же результатов по скорости и кинетической энергии, а по траектории и превысить показатели гарпуна, видоизмененного удлинением и утолщением.
4.4. Два ружья с одинаковой энергией выстрела.
В этом разделе мы проанализируем результаты выстрела двух ружей, передающих одинаковую кинетическую энергию гарпунам, естественно без учета эффектов подброса и волнообразных колебаний гарпунов.
Прообразом первого ружья послужило пневматическое с расположением рукоятки на 2/3 длины ствола. Диаметр гарпуна 8 мм, а его длина 76 см. При закачке 25 кг и коэффициенте полезного действия 75% гарпун получает энергию 108 Дж. Кончик гарпуна при окончания разгона отстоит от рукоятки на расстоянии 1,2 м.
Вторым ружьем выберем арбалет с длиной гарпуна 1,15 м и диаметром 6,25 мм, так как только арбалет можно зарядить столь тонким гарпуном такой длины. Фирма-производитель гарантирует получение гарпуном 108 Дж при использовании 18-ти миллиметровых тяг. Расстояние от кончика гарпуна до рукоятки при окончании разгона 1,8 м.
Поскольку гарпуны имеют приблизительно одинаковую массу (298 г и 275 г), то имея равные кинетические энергии, будут иметь и почти равные начальные скорости.
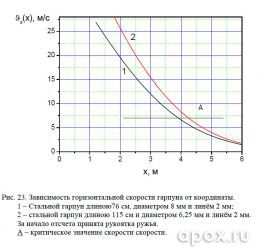
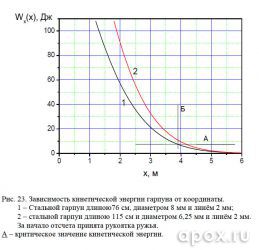
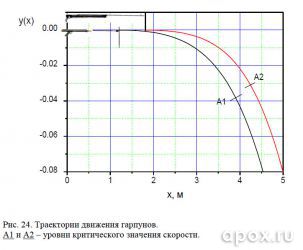
График, приведенный на рисунке 23, показывает, что убойная дистанция арбалета больше на 34 см. Если же анализировать зависимость кинетической энергии от координаты (см. рис. 24), то дистанция уверенного поражения увеличивается на 28 см. Как видим, преимущество хоть и есть, но незначительное. Если же анализировать уровень энергии арбалета на критической дистанции пневмата (сечение Б), то прирост составит 50%, а это уже существенная прибавка для уверенного поражения цели.
Анализ траекторий движения двух гарпунов показывает, что на критической для пневмата дистанции отклонение гарпуна от прямолинейной траектории на 3 см больше, нежели у арбалета (см. рис. 24).
Таким образом, последние факты объясняют преимущество применения арбалета на открытой воде. Но здесь стоит еще раз заметить, что наши исследования предполагали рассмотрение идеальных ружей, которые не имеют подброса, гарпуны жестко фиксированы на всем протяжении
разгона, а флажки не нарушают осевую симметрию. В реальной ситуации отсутствие направляющей гарпуна на арбалете и верхнее расположение флажка увеличивает отклонение от прямолинейной траектории на 2-3 см, а подброс «недобросовестного» пневмата заставляет охотника целиться с занижением на коротких дистанциях стрельбы.
Также следует сказать, что указанные преимущества арбалета достигаются не за счет меньшего сопротивления водной среды движению гарпуна. По скоростным и энергетическим характеристикам в системе отсчета связанной с острием в момент окончания разгона длинный и тонкий гарпун проигрывает на всей дистанции полета толстому и короткому.
Преимущество же достигается счет того, что острие в момент окончания разгона выдвинуто на 60 см дальше, чем у пневмата.
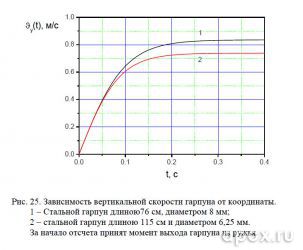
Кроме того, имея б’ольшую площадь осевого сечения гарпун арбалета падает (движется в вертикальном направлении) медленнее, чем гарпун пневмата (см. рис. 25). Напомним, что построенные математические модели не учитывают эффекты стабилизации гарпуна как за счет собственной длины, поэтому в реальных условиях будет возникать и стабилизирующий момент,
который у данного арбалетного гарпуна выше на 20%.
Не агитируя «за Советскую власть», то есть, не перечисляя преимуществ и недостатков каждого типа ружей, скажем: «Хотите далеко стрелять – приобретите длинное ружье!». Расчеты показывают: насколько бы не было перекачано или не обвешано дополнительной резиной короткое ружье, оно проиграет длинному. Ведь удлиняя всю конструкцию, мы получаем еще и дополнительный ход поршня или резиновых тяг, а значит и увеличение начальной кинетической энергии.
5. Заключение.
В данной работе мы постарались рассмотреть особенности полета гарпунов, выпущенных из подводного ружья. Варьируя плотностью материала, диаметром и длиной были определены наиболее выгодные изменения, которые следует вносить в конструкцию гарпуна для получения наилучших результатов стрельбы.
По большему счету, работа не открывает каких либо сногсшибательных фактов – большинство приведенных теоретических результатов уже получены охотниками экспериментальным путем. Но имея представленные математические выкладки и расчетную программу (прилагаемый файл Exel ), можно провести количественные (а не просто качественные) расчеты и, возможно, избежать ненужных ошибок при приобретении или модернизации оружия.
В прилагаемом файле формата Exel рассчитываются зависимости исследуемых величин по заданным параметрам гарпуна и ружья. Истинным аргументом является координата х, а все остальные величины – это функции. Но так как колонка времени взаимосвязана с координатой, то справедливыми будут и зависимости скорости, энергии, силы и т.д. от времени. Также справедливой будет и зависимость y(x) – траектория движения гарпуна. Колонку G «t(x)+t выхода», в которой рассчитано суммарное время с момента начала действия на гарпун силы и до достижения гарпуном определенной дистанции лучше всего использовать только для построения графика подлетного времени tподлета(x). Следует учесть, что в расчетах за начало отсчета принято положение острия гарпуна в момент окончания разгона, поэтому для вычисления реальной дистанции следует добавить расстояние до рукоятки ружья. При желании можно обойтись без задания КПД, силы зарядки и хода поршня ружья, введя значение начальной скорости или кинетической энергии в соответствующие ячейки.
Все ячейки не защищены от изменений с той целью, чтобы любой желающий мог видеть заложенные принципы расчета и формулы. В таблицах есть несколько скрытых колонок, которые подсчитывают интегральные суммы.
Рекомендации.
Настоятельно не рекомендуем проводить расчеты с помощью калькулятора, так это может нанести существенный вред Вашему здоровью. Строить графики в Exel, на наш взгляд, не нужно, так как анализировать их будет достаточно хлопотно. Для этой цели мы использовали программу Origin; можно также применить специализированные программы типа Mapl, Mathcad и др.
Литература.
1. Блинов А.Д. Курс артиллерии. Внешняя баллистика метрология в артиллерии. Полная подготовка данных для стрельбы.. –М.: Воениздат, 1948. – 288 с.
2. Белевич М.Ю. Гидромеханика. Основы классической теории. Учебное пособие - Санкт-Петербург: РГГМУ, 2006.- 213 с.
3. Дехтярь В.Г., Петров В.И. Гидродинамика баллистических ракет подводных лодок: монография –Миасс: ФГУП «РГЦ КБ им. какд. В.П. Макеева», 2004. 256с.: ил.
4. Корпачев В.П. Теоретические основы водного транспорта леса. Изд. "Академия Естествознания", 2009.
5. Зельдович Я.Б., Яглом И.М. Высшая математика для начинающих физиков и техников. - М.: Наука, 1982. – 510 с.
6. Коробейников А.В., Митюков Н.В. Баллистики старел по данным археологии: введение в проблемную область. –Ижевск: Изд-во НОУ КИТ, 2007, –140 с.
7. Озерецковский Л., Гребнев Д., Головко К., Альтов Д. // Травматический диагноз. Калашников. Оружие, Боеприпасы, снаряжение, №8, 2009, с.68.
Сергей Коваленко (kovalsky)
канд. физ.-мат. наук





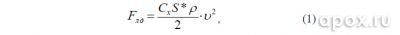
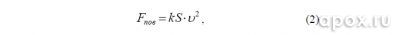
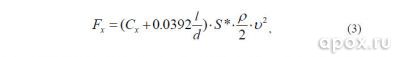
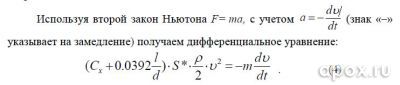
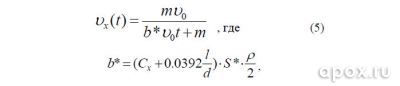
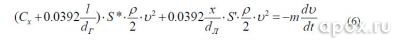
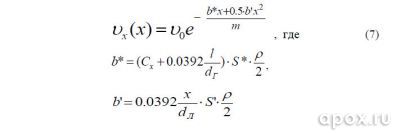
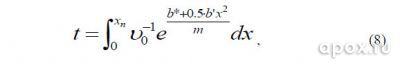
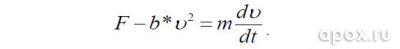
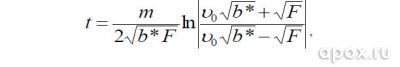
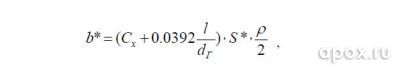
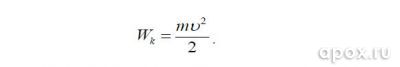
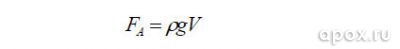
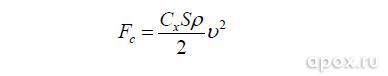
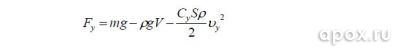
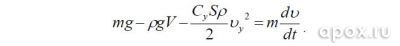
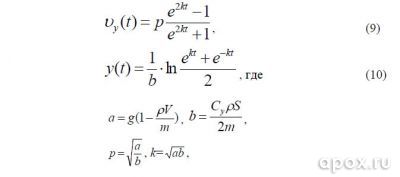

 ,
,




33 Комментария
Рекомендуемые комментарии